Energy-based Generative Adversarial Network
公和众和号:EDPJ(进 Q 交流群:922230617 或加 VX:CV_EDPJ 进 V 交流群)
目录
0. 摘要
2. EBGAN 模型
2.1 目标函数
2.2 解决方案的最优解
2.3 使用自动编码器
2.3.1 与正则化自动编码器的关联
2.4 排斥正则化器
4. 实验
0. 摘要
我们介绍了 “基于能量的生成对抗网络” 模型(EBGAN),该模型将鉴别器视为一个能量函数,该函数为数据流形附近的区域分配低能量,而为其他区域分配更高的能量。与概率型 GAN 类似,生成器被训练以生成具有最小能量的对比样本,而鉴别器被训练来为这些生成的样本分配高能量。将鉴别器视为能量函数允许使用各种架构和损失函数,除了通常的具有逻辑输出的二元分类器之外。其中,我们展示了 EBGAN 框架的一种实例,使用自动编码器架构代替了鉴别器,其中能量是重构误差。我们展示了这种形式的 EBGAN 在训练期间表现比常规 GAN 更稳定。我们还展示了可以训练单一尺度的架构以生成高分辨率图像。
代码:https://github.com/1Konny/EBGAN-pytorch
2. EBGAN 模型
设 p_data 为生成数据集的概率密度。生成器 G 被训练以从随机向量 z(例如,从已知分布 p_z ~ N(0,1) 中抽样)生成样本 G(z),例如一张图像。鉴别器 D 接受真实或生成的图像,并相应地估计能量值 E ∈ R,如后文所述。为简单起见,我们假设 D 产生非负值,但只要这些值在下限有界,分析仍然成立。
2.1 目标函数
鉴别器的输出通过一个目标函数,以塑造能量函数,为真实数据样本分配低能量,为生成的(“伪造的”)样本分配高能量。在这项工作中,我们使用一个边缘损失,但正如 LeCun 等人(2006年)中所解释的,还有许多其他选择。与概率 GAN(Goodfellow等人,2014年)中所做的类似,我们使用两种不同的损失,一种用于训练 D,另一种用于训练 G,以便在生成器远离收敛时获得更好的质量梯度。
给定正边界(margin) m,数据样本 x 和生成样本 G(z),鉴别器损失 L_D 和生成器损失 L_G 定义为:
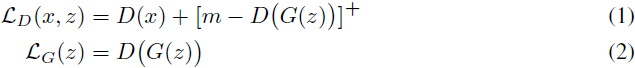
其中 [·]+ = max(0,·)。将 LG 相对于 G 的参数最小化类似于最大化 LD 的第二项。当 D(G(z)) 大于等于 m 时,它具有相同的最小值,但是在这种情况下梯度是非零的。
2.2 解决方案的最优解
在这一部分中,我们对第 2.1 节中提出的系统进行理论分析。我们展示,如果系统达到纳什均衡,那么生成器 G 生成的样本与数据集的分布不可区分。 本节在非参数设置中完成,即我们假设 D 和 G 具有无限容量。
给定生成器 G,令 p_G 为 G(z) 的密度分布,其中 z ~ p_z。换句话说,p_G 是由 G 生成的样本的密度分布。
我们定义
![]()
![]()
我们训练鉴别器 D 以最小化 V,生成器 G 以最小化 U。 系统的纳什均衡是一个满足以下条件的对(G*,D*):

定理1. 如果 (G*,D*) 是系统的纳什均衡,那么几乎处处 p_G* = p_data ,并且 V(G*,D*) = m。
(结合公式 1、2 和积分公式推导获得,证明见原文)
定理2. 该系统存在一个纳什均衡,其特征为(a) p_G* = p_data(几乎处处),以及(b) 存在常数 γ ∈ [0,m],使得 D*(x) = γ (几乎处处)。
2.3 使用自动编码器
在我们的实验中,鉴别器D被构建为一个自动编码器:
![]()

EBGAN 模型的自动编码器鉴别器的图表如图 1 所示。选择自动编码器作为 D 可能乍一看似乎是任意的,然而我们假设这在概念上比二元逻辑网络更具吸引力:
- 与使用单个目标信息训练模型的二元逻辑损失不同,基于重构的输出为鉴别器提供了多样的目标。使用二元逻辑损失,只有两个目标是可能的,因此在一个小批量内,对应于不同样本的梯度很可能远离正交。这导致训练效率低下,并且在当前硬件上通常无法减小小批量大小。另一方面,重构损失可能会在小批量内产生非常不同的梯度方向,允许更大的小批量大小而不损失效率。
- 自动编码器传统上用于表示基于能量的模型,并且自然产生。在使用一些正则化项进行训练时(参见第 2.3.1 节),自动编码器具有学习能量流形的能力,而无需监督或负样本。这意味着即使 EBGAN 自动编码模型被训练用于重构真实样本,鉴别器也通过自身发现数据流形。相反,没有来自生成器的负样本,用二元逻辑损失训练的鉴别器变得无意义。
2.3.1 与正则化自动编码器的关联
在训练自动编码器时的一个常见问题是模型可能学到的仅仅是一个恒等函数,这意味着它为整个空间分配了零能量。为了避免这个问题,必须推动模型对数据流形之外的点给予更高的能量。理论和实验结果通过对潜在表示进行正则化来解决了这个问题(Vincent 等人,2010;Rifai等人,2011;MarcAurelio Ranzato&Chopra,2007;Kavukcuoglu等人,2010)。 这些正则化器旨在限制自动编码器的重构能力,使其只能为输入点的较小部分分配低能量。
我们认为 EBGAN 框架中的能量函数(鉴别器)也被视为通过生成对比样本的生成器进行正则化,鉴别器应该为其赋予高重构能量。我们进一步认为,从这个角度来看,EBGAN 框架允许更大的灵活性,因为:(i)正则化器(生成器)是完全可训练的,而不是手工制作的;(ii)对抗性训练范式使产生对比样本和学习能量函数的二元性之间的直接交互成为可能。
2.4 排斥正则化器
我们提出了一个 “排斥正则化器”,它很好地适应 EBGAN 自动编码器模型,有意地阻止模型生成聚集在 p_data 的一个或仅有几个模式中的样本。 另一种技术 “小批量鉴别” 由Salimans等人(2016)从相同的哲学中发展而来。
实施排斥正则化器涉及一个在表示级别运行的 “拉开项”(Pulling-away Term,PT)。形式上,让 S ∈ R^(s x N) 表示从编码器输出层获取的一批样本表示。让我们将 PT 定义为:
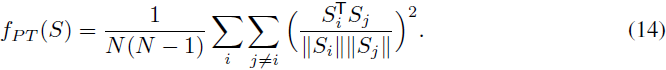
PT 在一个小批量上运行,并试图使成对的样本表示正交化。它受到之前工作的启发,该工作展示了类似于自动编码器的模型中编码器的表示能力,如 Rasmus 等人(2015)和 Zhao 等人(2015)。选择余弦相似度而不是欧氏距离的原因是使该项在下有界且对尺度不变。我们使用 “EBGAN-PT” 来指代使用该项训练的 EBGAN 自动编码器模型。请注意,PT 用于生成器损失而不是鉴别器损失。
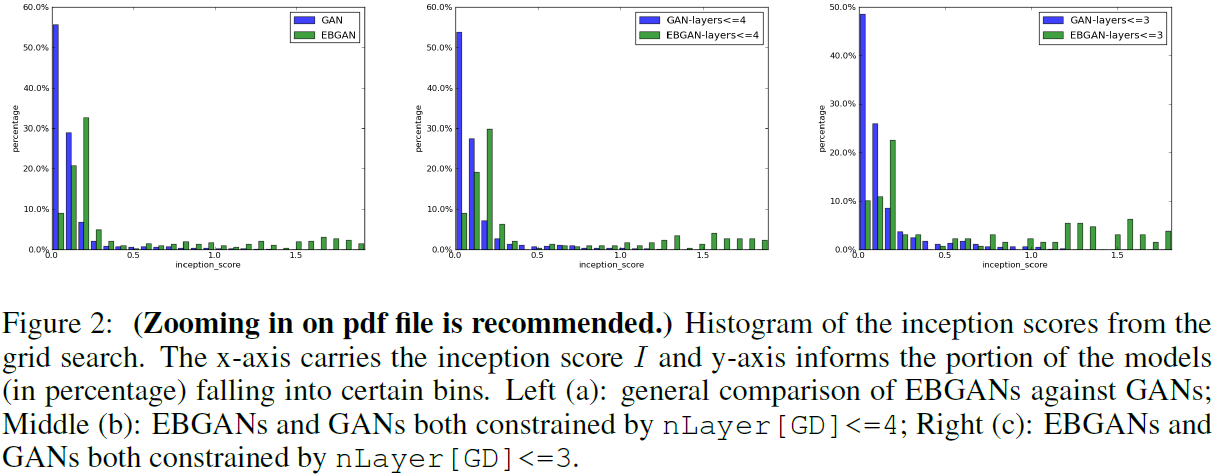
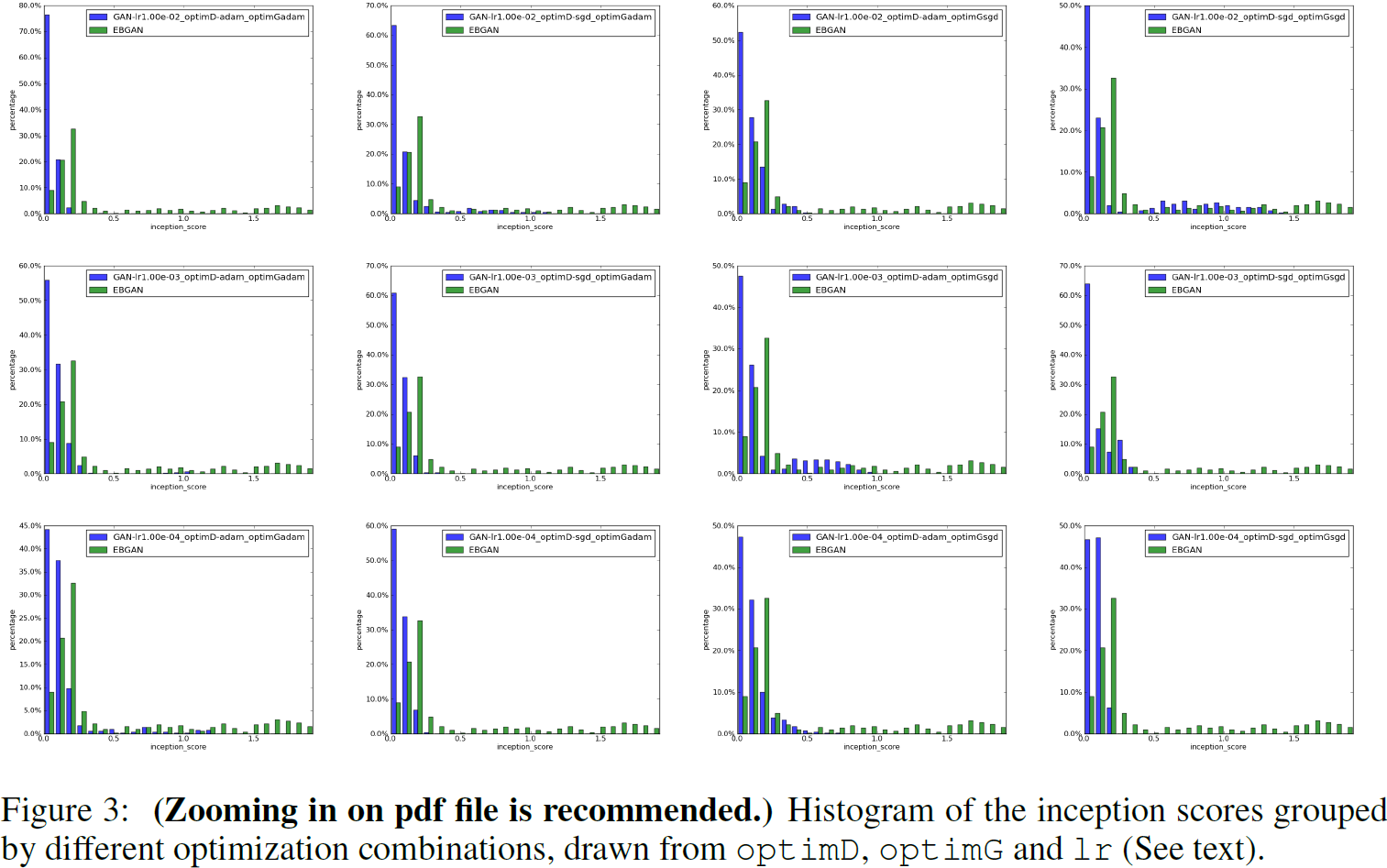
4. 实验




![[python] 过年燃放烟花](https://img-blog.csdnimg.cn/direct/0e9bbf7314694c23b32806bd57a6c284.png)